Abou Bakr Essadiq Redjil

Sample Space Reducing Process

By A.Redjil

Published:

Quantum Simulation
Figure 1. Sample Space Reducing Processs

Introduction

Many phenomenon are governed by a power law, where some characteristic of the system remains unchanged under re-scaling. Language is an example of such a system, where it has been observed empirically that the frequency of a word in a large corpus is inversely proportional to its rank, following Zipf's law \[ p(rank) \propto rank^{-1} \] Many models have been designed to explain the emergence of scaling in language. In this article, I will explore the sample-space reducing process model, which has been showen to produce perfect Zipf's law.

Sample Space Reducing Process

The sample space reducing process \(\phi\) is a stochastic process characterized by a shrinking sample space \(\Omega_t\). Initially, it contains a set of \(N\) ordered states \(\Omega_0 = \{N,N-1,\dots, 1\}\), each with a prior probability \(\pi_i\) of appearing. The process starts at the highest possible state \(X_0 = N\). At each discrete time step \(t>0\), the process jumps randomly to a lower state \(X_{t+1} < X_{t}\), following two rules:

After every jump, the sample space \(\Omega\) shrinks, making the possible jumps more constrained:

\[ |\Omega_0| > |\Omega_{X_t}| > \dots > |\Omega_{X_T}| \]

This setup reflects how language is produced. When a word is chosen in a text, the next words are constrained by the language’s grammar, semantics, and pragmatics. For instance, the sentence Colorless green ideas sleep furiously is grammatically correct, but semantically nonsensical. In this sense, the sample space of possible words shrinks with each word chosen.

Using a uniform prior probability of state occurance \(\pi_i=\dfrac{1}{N}\), and uniform transition probability over the lower states \(p(i\mid j) = \dfrac{1}{j-1}\), we can show that the probability of state visits \(\mathcal{P}(X_{t>0} = i) =p(i)\) follows an exact Zipf's law

\[ p(i) = i^{-1} \]

Numerical Simulation

Numerical simulations of the process using \(N=10^4\) states using \(M=10^6\) restarts, show that the state visits frequency indeed follow Zipf's law.

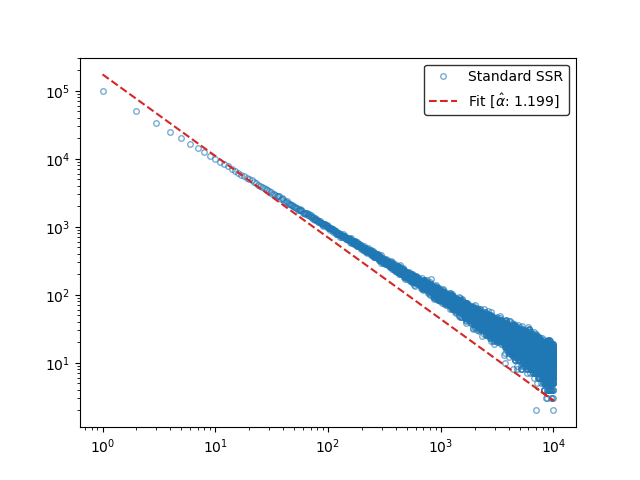
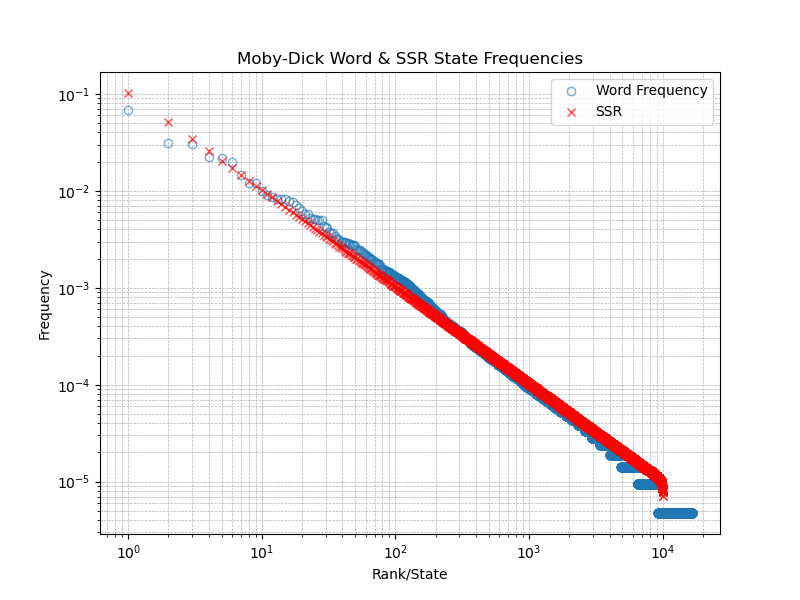
SSR state visits
Figure 2. Sample Space Reducing Processs state visits distrubution, the data was fitted using powerlaw package

Plotting the state visits frequency \(N=10^4\) states for \(M=10^6\) restarts along with word count of the words from Moby Dick

SSR state visits
Figure 3. Sample Space Reducing Processs state visits distrubution, the data was fitted using powerlaw package

Conclusion

Despite its simplicity SSR processes provide a simple yet powerful explaination of the emergence of Zipf's law in language. By modeling how the space of possible words shrinks over time.